HARFA: SCREENSHOTS AND TUTORIALS: OVERVIEW   Filtration Overview The filtration is founded on the combination of pixels (their colour information) in small neighbourhood by certain manner, which results in a new, changed picture. This neighbourhood is usually of square shape and is called filtration matrix. The result of pixel combination is assigned to the pixel which lies in the centre of the filtration matrix. The simplest way of combining pixels is multiplying pixels by proper coefficients of filtration matrix, adding to the sum of multiplied pixels and assigning result to the pixel in the centre of the filtration matrix. This operation is a discrete convolution, and filters, which work by this method are called convolution filters.          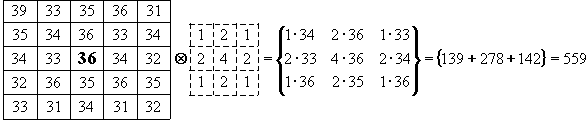The scheme of discrete convolution with filtration matrix 3x3 (marked by dashed border). Changed pixel of original image is highlighted. It's new value (after convolution) operation is 559. To display this value (0-255), some normalization is necessary. We achieve this dividing result by the sum of coefficients of filtration matrix (16). Then resulting value is 35. Convolution filters, which work by multiplying and adding, are called linear filters (Sobel filters, derivative filters). But there are filters that work by sorting followed by the selection of the resulting value by some criteria (minimum, maximum, average, median). These filters are called rank value filters (median filter, Kuwahara filter). We can write the resulting value of the convolution operation into the original image or into the new image. In the first case the result of convolution is calculated as the sum of unchanged pixels, and pixels, which were already changed by convolution operation. Filters which form new images, are called recursive filters. In HarFA there are only filters, which form new image. Furthemore, it is necessary to mention the problem of borders. On the borders of image, convolution sum can't be calculated, because corresponding pixels are missing.          The demostration of problem of calculation of convolution sum on border of an image. Regular solution of this is to fill missing values by values of opposite border. But this is not commonly used. Usually, border of half size of the filtration matrix is added to an image. It's filled up by zeros or by values, which are extrapolated from existing image in some way. HarFA enables computation of the convolution sum just for pixels with necessary surrounding pixels. Remaining border pixels are removed after filtration, e.g. image will be cropped.          The solution of 'border problem' used in HarFA, dark border will be removed. Previous Next