Fractal Physics used for the description of conservative forces of fractal fields in the Euclidean space is presented. The physical quantities used for the description of different properties of physical reality (electrical, gravitational, thermal, acoustic, etc.) are defined. The mathematic of fractal–Cantorian geometry is used for the description of properties of the electrical field of systems with different mass distribution, electrical properties of semiconductors, thermal properties of ideal gas and properties of high-energy particles.

The fractals can be described using fractal measure (K) and fractal dimension (D). Fractal measure defines in practice the magnitude of the coverage of space using the elementary cell (e.g. percentage coverage), while fractal dimension describes the trend of change of coverage as a function of size of measuring cell (its radius can be bigger or smaller than this radius of elementary cell). Fractal dimension can vary between two limits:
– for D = 0 the change of structure of fractal as the function of size of measure will be maximum (in the real world e.g. the idealised objects mass point or point charge represent such situation),
– for D = E, where E is Euclidean dimension the change of fractal structure will not depend on the change of measure (in the real world e.g. the idealised object rigid body represents this situation).

Literature

Mathematical Apparatus
The density of fractal physical quantity ro(r), (e.g. density of electric charge e or mass m) in the E - dimensional Euclidean space En (E = n) can be defined

,

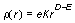where r is the radius of elementary quantity, K is a fractal measure and D a fractal dimension. The change in the mean value of density ro(r) of physical field with the change of size r by dr can be determined by the Gauss-Ostrogradsky law

.

The vector E defines the intensity of physical field of scalar r(r). The radial component of intensity Er (when field is point-symmetric), can be written

.

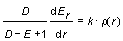The physical field E and the potential V are related as follows

,

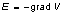so both quantities are determined by a density ro(r) distribution

,

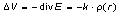where A is so called Laplace operator. This equation can be written for the radial distribution of density physical field ro(r) as

.

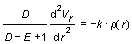From the density of the quantity ro(r) we can determine the radial field intensity Er and the corresponding potential Vr of physical (e.g. electric or gravitational) field

, .

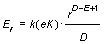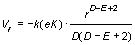From the density of the quantity and from the potential of the physical field the density of the energy



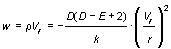
can be also determined.